 |
|
Você está aqui: GoLang ::: Dicas & Truques ::: Geometria, Trigonometria e Figuras Geométricas |
||
Como calcular a equação reduzida da reta em GoLang dados dois pontos pertencentes à retaQuantidade de visualizações: 994 vezes |
||
|
Nesta dica de Go veremos como calcular a equação reduzida da reta quando temos dois pontos pertencentes à esta reta. Não, nessa dica não vamos calcular a equação geral da reta, apenas a equação reduzida. Em outras dicas do site você encontra como como isso pode ser feito. Para relembrar: a equação reduzida da reta é y = mx + n, em que x e y são, respectivamente, a variável independente e a variável dependente; m é o coeficiente angular, e n é o coeficiente linear. Além disso, m e n são números reais. Com a equação reduzida da reta, é possível calcular quais são os pontos que pertencem a essa reta e quais não pertencem. Vamos começar então analisando a seguinte figura, na qual temos dois pontos que pertencem à uma reta: 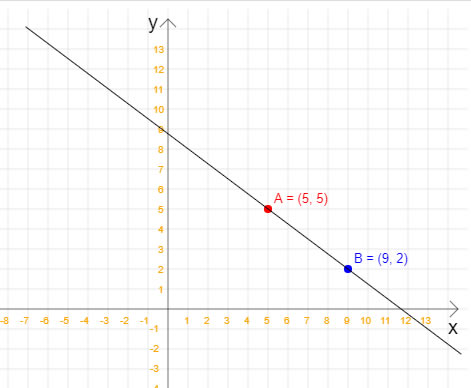 Note que a reta da figura passa pelos pontos A(5, 5) e B(9, 2). Então, uma vez que já temos os dois pontos, já podemos calcular a equação reduzida da reta. Veja o código GoLang completo para esta tarefa:
Ao executar este código GoLang nós teremos o seguinte resultado: Coordenada x do primeiro ponto: 5 Coordenada y do primeiro ponto: 5 Coordenada x do segundo ponto: 9 Coordenada y do segundo ponto: 2 Equação reduzida: y = -0,75x + 8,75 Para testarmos se nossa equação reduzida da reta está realmente correta, considere o valor 3 para o eixo x da imagem acima. Ao efetuarmos o cálculo:
temos o valor 6.5 para o eixo y, o que faz com que o novo ponto caia exatamente em cima da reta considerada na imagem. |
||
 Link para compartilhar na Internet ou com seus amigos: |
||
Veja mais Dicas e truques de GoLang |
Dicas e truques de outras linguagens |
|
Java - Como comparar strings em Java usando os métodos compareTo() e compareToIgnoreCase() da classe String |
E-Books em PDF |
||||
|
||||
|
||||
Linguagens Mais Populares |
||||
|
1º lugar: Java |
