 |
|||||
 Planilha Web - Planilhas e Calculadoras online para estudantes e profissionais de Engenharia Civil, Engenharia Elétrica e Engenharia Mecânica. |
|||||
|
|||||
| Voltar para Calculadoras de Matrizes |
Calculadora de Determinante |
| Informe os elementos da matriz separados por espaços (pressione Enter para uma nova linha) e clique o botão Calcular Determinante. |
O que é o Determinante?Na Matemática e na Álgebra Linear, o determinante é uma função matricial que associa a cada matriz quadrada um escalar, ou seja, o determinante é uma função que transforma uma matriz quadrada em um número real.O determinante, ou melhor, a função determinante, permite saber se a matriz tem ou não inversa (matriz inversa), pois, as matriz que não tem inversa, são precisamente aquelas cujo determinante é igual a 0. Se o determinante for diferente de zero, então a matriz é uma matriz invertível. O determinante de uma matriz A é denotado por det(A), det A ou |A|. Como o Determinante de uma matriz é calculado?O cálculo do determinante de uma matriz só pode ser realizado quando a matriz é quadrada, ou seja, ela possui o mesmo número de linhas e colunas. Assim, há três situações:1) Determinante de uma matriz de ordem 1: Para o caso de uma matriz de ordem 1, ou seja, uma matriz 1x1 (uma linha e uma coluna), o determinante é o próprio valor do único elemento da matriz. 2) Determinante de uma matriz de ordem 2: No caso de matrizes de ordem 2, ou seja, 2x2, o cálculo do determinante pode ser realizado da seguinte forma: 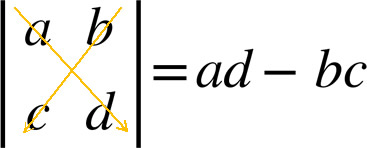 3) Determinante de uma matriz de ordem N (N > 2): Calcular o determinante de uma matriz de ordem maior que 2 exige uma pouco mais de esforço. Há um caso especial, que são as matrizes 3x3, que podem ter o seu determinante calculado facilmente usando-se a Regra de Sarrus, ou Método de Sarrus (chamado também de Esquema de Sarrus), conforme demonstramos nesse link: Java para Álgebra Linear - Como calcular o determinante de uma matriz 3x3 usando a regra de Sarrus em Java. Sabendo-se que a Regra de Sarrus é restrita apenas às matrizes quadradas de ordem 3, chegamos então ao Teorema de Laplace, que serve para calcular o determinante de matrizes de qualquer ordem. É muito comum o desenvolvimento de algorítimos recursivos para realizar o cálculo. No entanto, é preciso ter muito cuidado, pois o computador de poder computacional médio pode demorar semanas para encontrar o determinante de uma matriz 25x25, e milhares de anos para matrizes de ordem maior que isso. Nossa Calculadora de Determinante usa uma versão recursiva do Teorema de Laplace, escrita em JavaScript, para o cálculo do determinante de matrizes de ordem maior que 2, e esse processamento é feito diretamente no navegador do usuário. Dessa forma, tenha cuidado ao inserir os dados da matriz. Uma matriz de ordem muito alta poderá travar ou congelar o seu browser ou computador por vários minutos, forçando-o, até mesmo, a reiniciar. |
E-Books em PDF |
||||
|
||||
|
||||
Linguagens Mais Populares |
||||
|
1º lugar: Java |
