C ::: Dicas & Truques ::: Strings e Caracteres |
Como criar sua própria função substring() para obter uma substring a partir de uma string em CQuantidade de visualizações: 17002 vezes |
Em algumas situações precisamos obter uma substring a partir de uma string. A linguagem C já fornece algumas funções que tornam isso possível. No entanto, nenhuma destas funções permite especificar o índice inicial da substring. Sendo assim, o trecho de código abaixo mostra como escrever uma função substring() que permite informar a string de origem, o índice inicial e a quantidade de caracteres que serão obtidos. O retorno da função será um ponteiro para a substring obtida:
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
char *substring(char *origem, int inicio, int quant){
char *res = origem;
int i = 0;
// posição inicial menor que 0 ou
// posição inicial muito exagerada?
if((inicio < 0) || (inicio > strlen(origem)))
inicio = 0;
// quantidade de caracteres muito exagerada?
if(quant > inicio + strlen(origem))
quant = strlen(origem) - inicio;
// obtem os caracteres desejados
for(i = 0; i <= quant - 1; i++){
res[i] = origem[inicio + i];
}
// marca o fim da string
res[i] = '\0';
return res;
}
int main(int argc, char *argv[])
{
char texto[] = "Gosto muito de C e C++";
// não podemos bagunçar a string original
char sub_temp[128];
strcpy(sub_temp, texto);
// 10 caracteres começando
// no índice 6
char *res = substring(sub_temp, 6, 10);
// exibe o resultado
puts(res);
// exibe a string original
puts(texto);
system("pause");
return 0;
}
Ao executar este código nós teremos o seguinte resultado: muito de C Gosto muito de C e C++ |
Delphi ::: Dicas & Truques ::: Strings e Caracteres |
Como substituir todas as ocorrências de uma substring em uma string em Delphi sem considerar maiúsculas e minúsculas usando a função ReplaceText()Quantidade de visualizações: 11993 vezes |
Algumas vezes precisamos substituir todas as ocorrências de uma substring em uma string mas não queremos diferenciar letras maiúsculas de letras minúsculas. Em Delphi isso pode ser feito com o auxílio da função ReplaceText(). Esta função requer a string na qual a substituição ocorrerá, a substring a ser substituída e a nova substring. O resultado será uma nova string resultante da substituição. Veja o exemplo:procedure TForm1.Button1Click(Sender: TObject); var frase: string; begin frase := 'PHP? Sim, eu gosto muito de PHP'; // vamos substituir todas as ocorrências de "PHP" por "Delphi' // sem considerar maiúsculas e minúsculas frase := ReplaceText(frase, 'Php', 'Delphi'); // vamos exibir o resultado ShowMessage(frase); end; Lembre-se de que esta função não diferencia maiúsculas e minúsculas. Não se esqueça de adicionar a unit StrUtils no uses do seu formulário. Para questões de compatibilidade, esta dica foi escrita usando Delphi 2009. |
jQuery ::: Dicas & Truques ::: Manipulação e Conteúdo Dinâmico |
Como adicionar conteúdo ao início de um elemento HTML usando a função prepend() do jQueryQuantidade de visualizações: 573 vezes |
|
O método prepend() permite adicionar conteúdo ao início de um elemento HTML. Este conteúdo pode ser um seletor, um elemento HTML, uma string HTML ou um objeto jQuery. Veja um trecho de código no qual adicionamos uma linha de texto no início de um parágrafo:
<script type="text/javascript">
<!--
function adicionarConteudo(){
var texto = "Mais uma linha.<br>";
$("#parag").prepend(texto);
}
//-->
</script>
O método prepend() opera em todos os elementos HTML retornados sob uma determinação condição. O retorno do método é um objeto jQuery que pode ser usado para fins de encadeamento de chamadas de métodos. |
PHP ::: PHP para Engenharia ::: Geometria Analítica e Álgebra Linear |
Como somar os elementos da diagonal principal de uma matriz em PHPQuantidade de visualizações: 2604 vezes |
|
A Matriz quadrada é um tipo especial de matriz que possui o mesmo número de linhas e o mesmo número de colunas, ou seja, dada uma matriz Anxm, ela será uma matriz quadrada se, e somente se, n = m, onde n é o número de linhas e m é o número de colunas. Em geral as matrizes quadradas são chamadas de Matrizes de Ordem n, onde n é o número de linhas e colunas. Dessa forma, uma matriz de ordem 4 é uma matriz que possui 4 linhas e quatro colunas. Toda matriz quadrada possui duas diagonais, e elas são muito exploradas tanto na matemática quanto na construção de algorítmos. Essas duas diagonais são chamadas de Diagonal Principal e Diagonal Secundária. A diagonal principal de uma matriz quadrada une o seu canto superior esquerdo ao canto inferior direito. Veja: 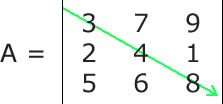 Nesta dica veremos como calcular a soma dos valores dos elementos da diagonal principal de uma matriz usando PHP. Para isso, só precisamos manter em mente que a diagonal principal de uma matriz A é a coleção das entradas Aij em que i é igual a j. Assim, tudo que temos a fazer é converter essa regra para código PHP. Veja um trecho de código PHP completo no qual pedimos para o usuário informar os elementos da matriz e em seguida mostramos a soma dos elementos da diagonal superior:
<?php
// vamos declarar e construir uma matriz de três linhas
// e três colunas
$matriz = array(
array(3, 7, 9),
array(2, 4, 1),
array(5, 6, 8)
);
// guarda a soma dos elementos na diagonal principal
$soma_diagonal = 0;
// vamos mostrar a matriz da forma que ela
// foi informada
echo "<br>";
// percorre as linhas
for($i = 0; $i < count($matriz); $i++){
// percorre as colunas
for($j = 0; $j < count($matriz[0]); $j++){
echo $matriz[$i][$j] . " ";
}
// passa para a próxima linha da matriz
echo "<br>";
}
// vamos calcular a soma dos elementos da diagonal
// principal
for($i = 0; $i < count($matriz); $i++){
for($j = 0; $j < count($matriz[0]); $j++){
if($i == $j){
$soma_diagonal = $soma_diagonal + $matriz[$i][$j];
}
}
}
// finalmente mostramos a soma da diagonal principal
echo "<br>A soma dos elementos da diagonal principal é: "
. $soma_diagonal;
?>
Ao executar este código PHP nós teremos o seguinte resultado: 3 7 9 2 4 1 5 6 8 A soma dos elementos da diagonal principal é: 15 |
Node.js ::: Dicas de Estudo e Anotações ::: Passos Iniciais |
Saiba o que é o Node.js e como baixar, instalar e testar seu funcionamento no WindowsQuantidade de visualizações: 1720 vezes |
|
O que é o Node.js Então todos os seus amigos estão comentando sobre Node.js e você não tem a mínima idéia do que se trata? Neste pequeno tutorial falaremos um pouco sobre essa ferramenta, faremos o download do instalador no Windows 10 (deve funcionar em outras versões também) e no final testaremos a instalação para termos certeza de que já estaremos prontos para desenvolver algumas idéias. O Node.js é uma plataforma server-side, ou seja, que executa do lado do servidor web e escrito a partir do Google Chrome's JavaScript Engine (V8 Engine), o motor de interpretação e/ou compilação de códigos JavaScript do navegador Google Chrome. Esta ferramenta foi desenvolvida por Ryan Dahl e desde então tem sido adotada em vários projetos web e sofre melhorias a cada versão. O objetivo principal do Node.js é facilitar o desenvolvimento de aplicações web que sejam mais rápidas e de fácil escalabilidade. Este web server (sim, o Node.js é um servidor web tal como o Apache Web Server, Tomcat, etc) usa um modelo direcionado a eventos (event-driven) e sem bloqueio de I/O, o que o torno leve e muito eficiente, perfeito para aplicações de tempo real e acesso intensivo a dados e que possam ser executadas em ambientes distribuidos. O Node.js é uma plataforma open source e cross-platform, ou seja, permite que nossos códigos rodem em diferentes sistemas operacionais com poucas ou nenhuma alteração. Além disso, aplicações Node.js são escritas em JavaScript e são executadas dentro do runtime do próprio Node.js. Para completar, esta ferramenta nos fornece uma extensa biblioteca de módulos JavaScript, o que simplifica ainda mais o desenvolvimento de aplicações web. Baixando e instalando o Node.js Para fazer o download do Node.js, direcione o seu navegador para a URL https://nodejs.org/en/download. Você encontrará os binários e instaladores para Windows, MacOS e Linux. Para este tutorial eu baixei o instalador para o Windows 64-bit Windows Installer (.msi), node-v12.16.3-x64.msi, com o tamanho de 18,8Mb. Execute o instalador e siga o passo-a-passo da instalação. Um detalhe importante é informar, para a instalação, um diretório que não contenha espaços. Veja:  Depois de escolhido o local de instalação, continue e logo você verá a seguinte tela:  Aqui o instalador nos informa que alguns módulos rpm precisam ser compilados com C/C++ antes de serem instalados. Se você quiser instalar tais módulos, algumas ferramentas tais como Python e o Visual Studio Build Tools deverão ser baixadas. Mas se você não quiser, não precisa se preocupar com isso agora. Apenas clique o botão Next e finalize a instalação. Testando a sua instalação do Node.js Finalizada a instalação, chegou a hora de fazermos o teste. Abra um janela de comando (cmd) e digite: node -v Opcionalmente você pode digitar --version em vez de -v. O resultado será a versão do Node.js que você acaba de instalar. Para concluir, vamos testar a interface de linha de comando do Node. Abra de novo a janela de terminal do Windows e digite apenas: node Agora você verá o sinal ">" aguardando os seus comandos. Digite algo como: console.log('Que beleza. O Node.js está pronto!'); Pressione a tecla Enter e o Node.js exibirá o conteúdo digitado. Para sair do comando de linha do Node e voltar para o terminal do Windows, basta pressionar Ctrl+D. Pronto! Agora você já pode ver nossas dicas de Node.js e dar continuidade aos seus estudos. |
Java ::: Dicas & Truques ::: Matemática e Estatística |
Regressão linear - Como calcular o coeficiente de correlação linear de Pearson em Java - Java para Machine LearningQuantidade de visualizações: 190 vezes |
 No estudo de Machine Learning, uma das primeiras ferramentas que aprendemos é Regressão Linear. E, para o bom entendimento da regressão linear, temos que aprender sobre o coeficiente de correlação linear, mais especificamente o coeficiente de correlação linear de Pearson. A fórmula do coeficiente de correlação linear de Pearson é: \[r_\text{xy} = \frac{n \sum x_i y_i - \sum x_i \sum y_i}{\sqrt{n \sum {x_i}^2 - \left(\sum {x_i}\right)^2} \cdot \sqrt{n \sum {y_i}^2 - \left(\sum {y_i}\right)^2}} \] Onde: x e y são os conjuntos de valores cuja correlação queremos testar. É claro que encontraremos algumas variações desta fórmula na internet e também em livros de estatística, mas o resultado é sempre o mesmo. A correlação de Pearson é uma técnica estatística para medir se duas variáveis estão linearmente relacionadas. Essa técnica também pode ser chamada de r de Pearson, correlação produto-momento de Pearson ou, mais coloquialmente, de correlação de Pearson. O r de Pearson é uma métrica que expressa a relação linear entre variáveis por meio de um número que vai de -1 a +1. Isto é, quanto mais próximo dos extremos (-1 ou +1), maior é a força da correlação. Por outro lado, valores próximos de zero indicam que a correlação é fraca. O sinal da correlação, por sua vez, indica a direção da relação entre variáveis. Se a correlação é positiva, então o aumento em uma variável implica o aumento na outra variável. Por outro lado, se a correlação é negativa, então o aumento em uma variável implica o decréscimo na outra variável. Veja agora o código Java completo no qual calculamps o coeficiente de correlação linear de Pearson a partir de valores x e y, dispostos em dois vetores, ou seja, dois arrays unidimensionais:
package estudos;
public class Estudos {
public static void main(String[] args) {
// vamos criar os vetores com os valores x e y
double x[] = {13, 32, 47, 54, 69, 73};
double y[] = {208, 184, 145, 14, 65, 32};
// as variáveis para os somatórios
double soma_x = 0, soma_y = 0, soma_x_quadrado = 0;
double soma_y_quadrado = 0, soma_x_vezes_y = 0;
// vamos percorrer os vetores e efetuar as somas
for (int i = 0; i < x.length; i++) {
// primeiro o somatório de x
soma_x = soma_x + x[i];
// agora o somatório de y
soma_y = soma_y + y[i];
// então o somatório de x^2
soma_x_quadrado = soma_x_quadrado + Math.pow(x[i], 2);
// e o somatório de y^2
soma_y_quadrado = soma_y_quadrado + Math.pow(y[i], 2);
// e finalmente o somatório de x*y
soma_x_vezes_y = soma_x_vezes_y + x[i] * y[i];
}
// vamos obter a quantidade de valores na observação
int n = x.length;
// e finalmente calculamos o coeficiente de correlação
// linear
double r_xy = ((n * soma_x_vezes_y) - (soma_x * soma_y)) /
(Math.sqrt((n * soma_x_quadrado) - Math.pow(soma_x, 2)) *
Math.sqrt((n * soma_y_quadrado) - Math.pow(soma_y, 2)));
// e mostramos o resultado
System.out.println("O coeficiente de correlação é: " +
r_xy);
}
}
Ao executar este código Java nós teremos o seguinte resultado: O coeficiente de correlação é: -0.8713675107044452 |
Java ::: Java para Engenharia ::: Geometria Analítica e Álgebra Linear |
Como calcular a norma ou módulo de vetores nos espaços R2 e R3 usando Java - Geometria Analítica e Álgebra Linear usando JavaQuantidade de visualizações: 2520 vezes |
|
Em Geometria Analítica e Álgebra Linear, a magnitude, norma, comprimento, tamanho ou módulo (também chamado de intensidade na Física) de um vetor é o seu comprimento, que pode ser calculado por meio da distância de seu ponto final a partir da origem, no nosso caso (0,0). Considere o seguinte vetor no plano, ou seja, no espaço bidimensional, ou R2: \[\vec{v} = \left(7, 6\right)\] Aqui este vetor se inicia na origem (0, 0) e vai até as coordenadas (x = 7) e (y = 6). Veja sua plotagem no plano 2D:  Note que na imagem já temos todas as informações que precisamos, ou seja, o tamanho desse vetor é 9 (arredondado) e ele faz um ângulo de 41º (graus) com o eixo x positivo. Em linguagem mais adequada da trigonometria, podemos dizer que a medida do cateto oposto é 6, a medida do cateto adjacente é 7 e a medida da hipotenusa (que já calculei para você) é 9. Note que já mostrei também o ângulo theta (__$\theta__$) entre a hipotenusa e o cateto adjacente, o que nos dá a inclinação da reta representada pelos pontos (0, 0) e (7, 6). Relembrando nossas aulas de trigonometria nos tempos do colegial, temos que o quadrado da hipotenusa é a soma dos quadrados dos catetos, ou seja, o Teorema de Pitágoras: \[a^2 = b^2 + c^2\] Como sabemos que a potenciação é o inverso da radiciação, podemos escrever essa fórmula da seguinte maneira: \[a = \sqrt{b^2 + c^2}\] Passando para os valores x e y que já temos: \[a = \sqrt{7^2 + 6^2}\] Podemos comprovar que o resultado é 9,21 (que arredondei para 9). Não se esqueça da notação de módulo ao apresentar o resultado final: \[\left|\vec{v}\right| = \sqrt{7^2 + 6^2}\] E aqui está o código Java que nos permite informar os valores x e y do vetor e obter o seu comprimento, tamanho ou módulo:
package arquivodecodigos;
import java.util.Scanner;
public class Estudos{
public static void main(String args[]){
Scanner entrada = new Scanner(System.in);
// vamos ler os valores x e y
System.out.print("Informe o valor de x: ");
double x = Double.parseDouble(entrada.nextLine());
System.out.print("Informe o valor de y: ");
double y = Double.parseDouble(entrada.nextLine());
// vamos calcular a norma do vetor
double norma = Math.sqrt(Math.pow(x, 2) + Math.pow(y, 2));
// mostra o resultado
System.out.println("A norma do vetor é: " + norma);
}
}
Ao executar este código nós teremos o seguinte resultado: Informe o valor de x: 7 Informe o valor de y: 6 A norma do vetor é: 9.219544457292887 Novamente note que arredondei o comprimento do vetor para melhor visualização no gráfico. Para calcular a norma de um vetor no espaço, ou seja, no R3, basta acrescentar o componente z no cálculo. |
Java ::: Coleções (Collections) ::: ArrayList |
Como adicionar todos os elementos de uma ArrayList ou coleção à uma outra ArrayList do Java usando o método addAll()Quantidade de visualizações: 15622 vezes |
Em algumas situações pode ser necessário adicionar todos os elementos de uma ArrayList ou outra coleção a uma determinada ArrayList já existente. Isso pode ser feito por meio do uso do método addAll() da classe ArrayList. Na versão 1.5 do Java, este método possui duas assinaturas. Veja a primeira:public boolean addAll(Collection<? extends E> c) Aqui nós podemos adicionar à uma ArrayList existente todos os elementos de uma determinada coleção, desde que, é claro, esta coleção implemente ou descenda de alguma classe que implemente a interface Collection. Note também o uso de genéricos na coleção a ser fornecida como argumento. É importante observar que, se passarmos uma coleção de tipos diferentes daquela na qual estamos chamando o método addAll() teremos um erro de compilação. Veja um exemplo no qual adicionamos todos os elementos de uma ArrayList no final de outra:
import java.util.ArrayList;
public class Estudos{
public static void main(String[] args){
// cria uma ArrayList que conterá strings
ArrayList<String> nomes = new ArrayList<String>();
// cria uma segunda ArrayList que conterá mais strings
ArrayList<String> nomes2 = new ArrayList<String>();
// adiciona itens na primeira lista
nomes.add("Carlos");
nomes.add("Maria");
nomes.add("Fernanda");
// adiciona itens na segunda lista
nomes2.add("Osmar");
nomes2.add("Zacarias");
// vamos adicionar os elementos da segunda lista
// no final da primeira lista
nomes.addAll(nomes2);
// vamos exibir o resultado
for(int i = 0; i < nomes.size(); i++){
System.out.println(nomes.get(i));
}
System.exit(0);
}
}
A segunda assinatura do método addAll() nos permite definir a posição no ArrayList alvo a partir da qual os elementos da coleção fonte serão adicionados. Veja: public boolean addAll(int index, Collection<? extends E> c) Eis um exemplo no qual inserimos os elementos de uma ArrayList a partir do segundo elemento da ArrayList alvo. Note que os itens existentes têm suas posições alteradas de forma a acomodar os novos elementos:
import java.util.ArrayList;
public class Estudos{
public static void main(String[] args){
// cria uma ArrayList que conterá strings
ArrayList<String> nomes = new ArrayList<String>();
// cria uma segunda ArrayList que conterá mais strings
ArrayList<String> nomes2 = new ArrayList<String>();
// adiciona itens na primeira lista
nomes.add("Carlos");
nomes.add("Maria");
nomes.add("Fernanda");
// adiciona itens na segunda lista
nomes2.add("Osmar");
nomes2.add("Zacarias");
// vamos adicionar os elementos da segunda lista
// a partir do segundo elemento da primeira lista
nomes.addAll(1, nomes2);
// vamos exibir o resultado
for(int i = 0; i < nomes.size(); i++){
System.out.println(nomes.get(i));
}
System.exit(0);
}
}
Como resultado da execução deste código nós teremos: Carlos Osmar Zacarias Maria Fernanda |
Android Java ::: android.widget ::: Button |
Como detectar um clique em um botão do Android usando setOnClickListener() e exibir uma mensagem AlertDialogQuantidade de visualizações: 1801 vezes |
|
O método setOnClickListener() nos permite definir a ação que será disparada ao clicarmos em um botão. Note que primeiro nós localizamos o botão no arquivo XML de layout usando o método findViewById() da classe View. Comece analisando o arquivo XML de layout no qual criamos um botão e o colocamos como filho de um elemento LinearLayout:
<?xml version="1.0" encoding="utf-8"?>
<LinearLayout xmlns:android="
http://schemas.android.com/apk/res/android"
android:orientation="vertical"
android:layout_width="fill_parent"
android:layout_height="fill_parent">
tools:context=".MainActivity">
<Button xmlns:android="
http://schemas.android.com/apk/res/android"
android:id="@+id/btn_enviar"
android:layout_width="wrap_content"
android:layout_height="wrap_content"
android:text="@string/btn_enviar"
android:textAllCaps="false"
/>
</LinearLayout>
E agora o código Java no arquivo MainActivity.java:
package com.example.estudosandroid;
import androidx.appcompat.app.AppCompatActivity;
import android.app.AlertDialog;
import android.content.DialogInterface;
import android.os.Bundle;
import android.view.View;
import android.widget.Button;
public class MainActivity extends AppCompatActivity {
@Override
protected void onCreate(Bundle savedInstanceState) {
super.onCreate(savedInstanceState);
setContentView(R.layout.activity_main);
// vamos detectar um clique no botão e exibir uma mensagem AlertDialog
Button button = (Button) findViewById(R.id.btn_enviar);
button.setOnClickListener(new View.OnClickListener(){
public void onClick(View view) {
AlertDialog dialogo = new
AlertDialog.Builder(MainActivity.this).create();
dialogo.setTitle("Aviso");
dialogo.setMessage("Esta é uma mensagem de aviso");
dialogo.setButton(AlertDialog.BUTTON_NEUTRAL, "OK",
new DialogInterface.OnClickListener() {
public void onClick(DialogInterface dialog, int which){
dialog.dismiss(); // fecha o AlertDialog
}
}
);
dialogo.show();
}
});
}
}
|
C++ ::: Fundamentos da Linguagem ::: Passos Iniciais |
C++ do básico ao avançado - Conheça a origem da linguagem C++Quantidade de visualizações: 13690 vezes |
|
C++ começou como uma versão expandida de C. As extensões C++ foram inventadas primeiramente por Bjarne Stroustrup, em 1979, no Bell Laboratories em Murray Hill, New Jersey. Ele inicialmente chamou a nova linguagem de "C com classes". Contudo, em 1983 o nome foi mudado para C++. Embora C fosse uma das linguagens preferidas e mais usadas para programação profissional em todo o mundo, a invenção de C++ se fez necessária devido a um fator de programação: o aumento da complexidade. No decorrer dos anos, programas de computador se tornaram maiores e mais complexos. Mesmo sendo uma excelente linguagem de programação, C tem seus limites. Em C, uma vez que um programa atinja a marca de 25.000 à 100.000 linhas de códigos, este se torna tão complexo que é difícil analisá-lo como um todo. A manutenção de seu código se torna um pesadelo. O propósito de C++ é quebrar esta barreira. A essência do C++ é permitir que programadores compreendam e gerenciem programas cada vez mais complexos. A maioria das adições feitas ao C por Stroustrup suportam a programação orientada a objetos, às vezes chamada de POO. Stroustrup afirmou que algumas das características da orientação a objetos de C++ foram inspiradas em uma linguagem chamada Simula67. Assim, C++ representa a combinação de dois métodos poderosos de programação. Desde que C++ foi inventada, ela já passou por três revisões importantes, com adições e modificações da linguagem. A primeira revisão ocorreu em 1985 e a segunda em 1990. A terceira ocorreu durante a padronização do C++. Há vários anos que este trabalho de padronização foi iniciado. Para esta finalidade, uma associação entre a ANSI (American National Standards Institute) e a ISO (International Standards Organization) resultou em um comitê de padronização. O primeiro documento contendo o padrão proposto foi criado em 25 de janeiro de 1994. Neste documento, o comitê ANSI/ISO C++ manteve as características definidas por Stroustrup e acrescentou algumas outras. Mas, no geral, este documento inicial refletiu o estado de C++ na época. Logo após a finalização do primeiro documento de padronização C++, um evento ocorreu e com ele a linguagem foi amplamente expandida: a criação da Standard Template Library (STL) por Alexander Stepanov. A STL é um conjunto de rotinas generícas que podemos usar para manipular dados. A STL não é somente poderosa e elegante, mas também muito extensa. |
Nossas 20 dicas & truques de programação mais populares |
|
CSS - Como definir uma imagem de fundo para a página HTML em CSS usando a propriedade background-image JavaScript - Como somar dias a uma data em JavaScript usando uma função personalizada adicionar_dias() que retorna um objeto Date |
Você também poderá gostar das dicas e truques de programação abaixo |
|
Delphi - Como retornar o caractere a partir de um determinado código ASCII em Delphi usando a função Chr() MySQL - Como retornar a hora atual no MySQL usando as funções CURTIME(), CURRENT_TIME e CURRENT_TIME() Java - Como remover um elemento de uma determinada posição do ArrayList do Java usando o método remove() Python - Como obter o resto de uma divisão de inteiros em Python - O operador módulo % da linguagem Python |
Nossas 20 dicas & truques de programação mais recentes |
Últimos Projetos e Códigos Fonte Liberados Para Apoiadores do Site |
|
Python - Como criar o jogo Pedra, Papel, Tesoura em Python - Jogo completo em Python com código comentado |
Últimos Exercícios Resolvidos |
E-Books em PDF |
||||
|
||||
|
||||
Linguagens Mais Populares |
||||
|
1º lugar: Java |






