PHP ::: Dicas & Truques ::: Arrays e Matrix (Vetores e Matrizes) |
Como testar se uma variável é do tipo array em PHP usando a função is_array()Quantidade de visualizações: 12065 vezes |
|
Em algumas situações nós precisamos verificar se uma determinada variável é do tipo array (vetor ou matriz). Em PHP esse procedimento pode ser feito com o auxílio da função is_array(), que recebe uma variável e retorna verdadeiro se ela é do tipo array e falso em caso contrário. Veja o código PHP completo para o exemplo:
<?php
// vamos criar um array de inteiros
$valores = Array(5, 2, 7, 1);
// vamos testar se a variável é do tipo array
if(is_array($valores)){
echo 'A variável $valores é do tipo array.';
}
else{
echo 'A variável $valores NÃO é do tipo array.';
}
?>
Ao executar este código PHP nós teremos o seguinte resultado: A variável $valores é do tipo array. |
Python ::: Desafios e Lista de Exercícios Resolvidos ::: Estruturas de Controle |
Exercício Resolvido de Python - Um comerciante comprou um produto e quer vendê-lo com um lucro de 45% se o valor da compra for menorQuantidade de visualizações: 1910 vezes |
|
Algoritmos Resolvidos de Python - Um comerciante comprou um produto e quer vendê-lo com um lucro de 45% se o valor da compra for menor Pergunta/Tarefa: Um comerciante comprou um produto e quer vendê-lo com um lucro de 45% se o valor da compra for menor que R$ 20,00; caso contrário, o lucro será de 30%. Elabore um algoritmo que leia o valor do produto e imprima o valor de venda para o produto. Sua saída deverá ser parecida com: Informe o valor do produto: 85 O valor de venda é: 110.5 Veja a resolução comentada deste exercício usando Python: Código para principal.py:
# método principal
def main():
# valor ler o valor do produto
valor = float(input("Informe o valor do produto: "))
# vamos calcular o valor de venda
if valor < 20:
valor_venda = valor + (valor * (45.0 / 100))
else:
valor_venda = valor + (valor * (30.0 / 100))
print("O valor de venda é: {0}".format(valor_venda))
if __name__== "__main__":
main()
|
Python ::: Desafios e Lista de Exercícios Resolvidos ::: Engenharia Civil - Cálculo Estrutural |
Exercícios Resolvidos de Python - Como calcular as reações de apoio, momento de flexão máxima e forças cortantes em uma viga bi-apoiada com carga distribuída retangular usando PythonQuantidade de visualizações: 1442 vezes |
|
Pergunta/Tarefa: Veja a seguinte figura: 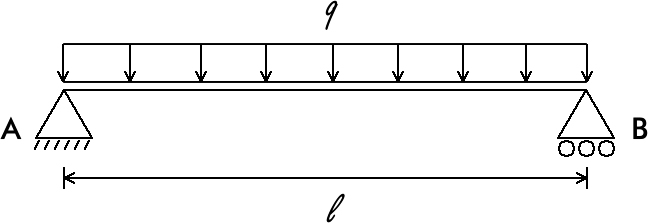 Nesta imagem temos uma viga bi apoiada com uma carga q distribuída de forma retangular a uma distância l. Para fins didáticos, vamos considerar que a carga q será em kN/m e a distância l será em metros. O apoio A é de segundo gênero e o apoio B é de primeiro gênero. Escreva um programa Python que solicita ao usuário que informe o valor da carga q e a distância l entre os apoios A e B. Em seguida mostre os valores das reações nos apoios A e B, o momento de flexão máxima da viga e o momento de flexão para uma determinada distância (que o usuário informará) a partir do apoio A. Mostre também as forças cortantes nos apoios A e B. Lembre-se de que, para uma carga distribuída de forma retangular, o diagrama de momento fletor é uma parábola, enquanto o diagrama de cortante é uma reta (com o valor zero para a força cortante no meio da viga). Sua saída deve ser parecida com: Valor da carga em kN/m: 10 Distância em metros: 13 A reação no apoio A é: 65.000000 kN A reação no apoio B é: 65.000000 kN O momento fletor máximo é: 211.250000 kN.m Informe uma distância a partir do apoio A: 4 O momento fletor na distância informada é: 180.000000 kN.m A força cortante no apoio A é: 65.000000 kN A força cortante no apoio B é: -65.000000 kN Veja a resolução comentada deste exercício usando Python:
# Algoritmo que calcula reação de apoio, momento fletor
# e força cortante em uma viga bi-apoiada em Python
# vamos importar o módulo Math
import math
# função principal do programa
def main():
# vamos pedir para o usuário informar o valor da carga
carga = float(input("Valor da carga em kN/m: "))
# vamos pedir para o usuário informar a distância entre os apoios
distancia = float(input("Distancia em metros: "))
# vamos calcular a reação no apoio A
reacao_a = (1.0 / 2.0) * carga * distancia
# vamos calcular a reação no apoio B
reacao_b = reacao_a
# vamos calcular o momento fletor máximo
flexao_maxima = (1.0 / 8.0) * carga * math.pow(distancia, 2.0)
# e mostramos o resultado
print("\nA reação no apoio A é: {0} kN".format(reacao_a))
print("A reação no apoio B é: {0} kN".format(reacao_b))
print("O momento fletor máximo é: {0} kN.m".format(flexao_maxima))
# vamos pedir para o usuário informar uma distância a
# partir do apoio A
distancia_temp = float(input("\nInforme uma distância a partir do apoio A: "))
# vamos mostrar o momento fletor na distância informada
if distancia_temp > distancia:
print("\nDistância inválida.")
else:
flexao_distancia = (1.0 / 2.0) * carga * distancia_temp * \
(distancia - distancia_temp)
print("O momento fletor na distância informada é: {0} kN.m".format(
flexao_distancia))
# vamos mostrar a força cortante no apoio A
cortante_a = (1.0 / 2.0) * carga * distancia
print("\nA força cortante no apoio A é: {0} kN".format(cortante_a))
# vamos mostrar a força cortante no apoio B
cortante_b = cortante_a * -1
print("A força cortante no apoio B é: {0} kN".format(cortante_b))
if __name__== "__main__":
main()
|
LISP ::: Dicas & Truques ::: Trigonometria - Funções Trigonométricas |
Como converter graus em radianos em LISP - Trigonometria em LISPQuantidade de visualizações: 966 vezes |
|
Quando estamos trabalhando com trigonometria na linguagem Common Lisp (e AutoLISP, para programadores AutoCAD), é importante ficarmos atentos ao fato de que todos os métodos e funções trigonométricas em Lisp recebem seus argumentos em radianos, em vez de graus. Nesta dica veremos como converter graus em radianos (sem a chatice de ficar relembrando regra de três). Veja a fórmula abaixo: \[Radianos = Graus \times \frac{\pi}{180}\] Agora veja como esta fórmula pode ser escrita em código LISP: ; programa LISP que converte graus em radianos (let((graus)(radianos)) ; valor em graus (setq graus 30) ; obtém o valor em radianos (setq radianos (* graus (/ pi 180))) ; mostra o resultado (format t "~F graus em radianos é ~F" graus radianos) ) Ao executarmos este código Common Lisp nós teremos o seguinte resultado: 30 graus convertidos para radianos é 0.5235987755982988 |
PHP ::: Dicas & Truques ::: Arquivos e Diretórios |
Como testar se um diretório existe em PHP usando a função file_exists()Quantidade de visualizações: 19008 vezes |
|
Em algumas situações nós precisamos verificar se um determinado diretório existe no sistema antes de efetuarmos alguma operação. Para isso nós podemos usar a função file_exists(). Esta função retorna um valor true se o diretório existir e false em caso contrário. Veja um código PHP completo demonstrando o seu uso:
<?php
$diretorio = "arquivo/imagens";
if(file_exists($diretorio)){
echo "O diretório já existe.";
}
else{
echo "O diretório não existe ainda.";
}
?>
|
C++ ::: Dicas & Truques ::: Trigonometria - Funções Trigonométricas |
Como calcular o cateto oposto dadas as medidas da hipotenusa e do cateto adjascente em C++Quantidade de visualizações: 1039 vezes |
|
Todos estamos acostumados com o Teorema de Pitágoras, que diz que "o quadrado da hipotenusa é igual à soma dos quadrados dos catetos". Baseado nessa informação, fica fácil retornar a medida do cateto oposto quando temos as medidas da hipotenusa e do cateto adjascente. Isso, claro, via programação em linguagem C++. Comece observando a imagem a seguir:  Veja que, nessa imagem, eu já coloquei os comprimentos da hipotenusa, do cateto oposto e do cateto adjascente. Para facilitar a conferência dos cálculos, eu coloquei também os ângulos theta (que alguns livros chamam de alfa) e beta já devidamente calculados. A medida da hipotenusa é, sem arredondamentos, 36.056 metros. Então, sabendo que o quadrado da hipotenusa é igual à soma dos quadrados dos catetos (Teorema de Pitógoras): \[c^2 = a^2 + b^2\] Tudo que temos que fazer é mudar a fórmula para: \[a^2 = c^2 - b^2\] Veja que agora o quadrado do cateto oposto é igual ao quadrado da hipotenusa menos o quadrado do cateto adjascente. Não se esqueça de que a hipotenusa é o maior lado do triângulo retângulo. Veja agora como esse cálculo é feito em linguagem C++:
#include <iostream>
#include <math.h>
#include <cstdlib>
using namespace std;
int main(int argc, char *argv[]){
float c = 36.056; // medida da hipotenusa
float b = 30; // medida do cateto adjascente
// agora vamos calcular o comprimento da cateto oposto
float a = sqrt(pow(c, 2) - pow(b, 2));
// e mostramos o resultado
cout << "A medida do cateto oposto é: " << a << "\n\n";
system("PAUSE"); // pausa o programa
return EXIT_SUCCESS;
}
Ao executar este código C++ nós teremos o seguinte resultado: A medida do cateto oposto é: 20.0009 Como podemos ver, o resultado retornado com o código C++ confere com os valores da imagem apresentada. |
Erlang ::: Dicas de Estudo e Anotações ::: Passos Iniciais |
Quer aprender a programar em Erlang? Comece instalando e configurando o ambiente de programação da ErlangQuantidade de visualizações: 744 vezes |
|
Nos dias atuais (2023), muitos estudantes de programação estão aprendendo novas linguagens usando os compiladores e interpretadores online. Esta é uma abordagem interessante, pois promove uma grande economia de tempo no que se refere à instalação e configuração dos ambientes de programação. No entanto, à medida que as aplicações começam a ficar mais complexas, é necessário termos o ambiente funcionando localmente. Por isso é importante sabermos instalar e configurar o ambiente de programação Erlang em nossa máquina. Como instalar a Erlang Nessa dica mostrarei como instalar e testar o ambiente de programação Erlang no Windows 10. Para isso, direcione o seu navegador para a URL https://www.erlang.org/downloads e localize o download apropriado para o Windows, a saber, Download Windows Installer. Para esta dica eu baixei o Erlang/OTP 25.3 (otp_win64_25.3.exe). Trata-se de um instalador com o tamanho de 126MB. A instalação é simples e, em geral, só precisamos confirmar as sugestões que o instalador nos apresenta. Assim, basta pressionar o botão Next e aguardar a instalação ser finalizada. Após a conclusão da instalação nós precisamos adicionar o caminho "C:\Program Files\Erlang OTP\bin" na variável PATH do Windows, para que as ferramentas de linha de comando da Erlang sejam reconhecidas. Para isso, vá em Propriedades do Sistema -> Variáveis de Ambiente e adicione este caminho à variável PATH. Você pode fazê-lo tanto para o seu usuário quanto para o sistema. Como testar a atualização do ambiente de programação da Erlang Depois de atualizar a variável de ambiente PATH, abra uma nova janela de terminal e digite o seguinte comando: C:\Users\Osmar>erl -version Se tudo correu bem, você terá um resultado parecido com: Erlang (SMP,ASYNC_THREADS) (BEAM) emulator version 13.2 Parabéns! Você já está pronto para iniciar seus estudos em Erlang e todas as demais linguagens e ferramentas que compõem o seu ecosistema. |
Delphi ::: Win32 API (Windows API) ::: Formulários e Janelas |
Como usar a função GetWindow() da API do Windows para pesquisar e retornar um handle para uma janela baseado em seu título completo ou parcial usando DelphiQuantidade de visualizações: 15092 vezes |
|
Em algumas situações nós precisamos pesquisar e retornar um handle para uma janela baseado em seu título completo ou parcial, ou seja, gostaríamos de encontrar uma janela que contenha a palavra "sexo". Isso pode ser feito com o auxílio da função GetWindow() da API do Windows. Veja:
// função personalizada que permite encontrar uma janela
// baseado em seu título
function FindWindowByTitle(WindowTitle: string): Hwnd;
var
NextHandle: Hwnd;
NextTitle: array[0..255] of char;
begin
// vamos obter a primeira janela
NextHandle := GetWindow(Application.Handle, GW_HWNDFIRST);
while NextHandle > 0 do
begin
// vamos obter o título da janela
GetWindowText(NextHandle, NextTitle, 256);
// a janela contém o título que procuramos?
if Pos(Uppercase(WindowTitle), UpperCase(String(NextTitle))) <> 0 then
begin
Result := NextHandle;
Exit;
end
else
// vamos tentar a próxima janela
NextHandle := GetWindow(NextHandle, GW_HWNDNEXT);
end;
// não encontramos nada? vamos retornar um handle nulo
Result := 0;
end;
procedure TForm1.Button1Click(Sender: TObject);
var
handle: hwnd;
begin
// vamos localizar e fechar a Calculadora do Windows
// ou qualquer janela que contenha o texto "Calculadora"
handle := FindWindowByTitle('Calculadora');
if handle <> 0 then // encontramos a janela? vamos fechá-la
SendMessage(handle, WM_SYSCOMMAND, SC_CLOSE, 0)
else
ShowMessage('A janela pesquisada não foi encontrada');
end;
Neste exemplo nós pesquisamos uma janela que contenha a palavra "Calculadora" em seu título. Se encontrada, nós a fechamos com o auxílio da função SendMessage() e a mensagem WM_SYSCOMMAND com o valor SC_CLOSE para o parâmetro wParam. Para fins de compatibilidade, esta dica foi escrita usando Delphi 2009. |
C# ::: Dicas & Truques ::: Strings e Caracteres |
Como transformar uma string em um array de caracteres em C# usando o método ToCharArray()Quantidade de visualizações: 13820 vezes |
|
O método ToCharArray() da classe String da linguagem C# permite retornar um array de char contendo todos os caracteres presente na string original. Podemos tirar proveito disso para manipular os caracteres individuais de uma palavra, frase ou texto. Veja um código C# completo no qual demonstramos o seu uso:
using System;
namespace Estudos {
class Program {
static void Main(string[] args) {
string frase = "Gosto de C#";
Console.WriteLine("String original: " + frase);
// obtém um array de caracteres a partir da string
char[] letras = frase.ToCharArray();
// exibe os caracteres no array
for (int i = 0; i < letras.Length; i++) {
Console.WriteLine(letras[i]);
}
Console.WriteLine("Pressione uma tecla para sair...");
Console.ReadKey();
}
}
}
Ao executar este código C# nós teremos o seguinte resultado: String original: Gosto de C# G o s t o d e C # |
C ::: Dicas & Truques ::: Geometria, Trigonometria e Figuras Geométricas |
Como calcular o coeficiente angular de uma reta em C dados dois pontos no plano cartesianoQuantidade de visualizações: 3535 vezes |
|
O Coeficiente Angular de uma reta é a variação, na vertical, ou seja, no eixo y, pela variação horizontal, no eixo x. Sim, isso mesmo. O coeficiente angular de uma reta tem tudo a ver com a derivada, que nada mais é que a taxa de variação de y em relação a x. Vamos começar analisando o seguinte gráfico, no qual temos dois pontos distintos no plano cartesiano:  Veja que o segmento de reta AB passa pelos pontos A (x=3, y=6) e B (x=9, y=10). Dessa forma, a fórmula para obtenção do coeficiente angular m dessa reta é: \[\ \text{m} = \frac{y_2 - y_1}{x_2 - x_1} = \frac{\Delta y}{\Delta x} = tg \theta \] Note que __$\Delta y__$ e __$\Delta x__$ são as variações dos valores no eixo das abscissas e no eixo das ordenadas. No triângulo retângulo que desenhei acima, a variação __$\Delta y__$ se refere ao comprimento do cateto oposto e a variação __$\Delta y__$ se refere ao comprimento do cateto adjascente. Veja agora o trecho de código na linguagem C que solicita as coordenadas x e y dos dois pontos, efetua o cálculo e mostra o coeficiente angular m da reta que passa pelos dois pontos:
#include <stdio.h>
#include <stdlib.h>
int main(int argc, char *argv[]){
// coordenadas dos dois pontos
float x1, y1, x2, y2;
// guarda o coeficiente angular
float m;
// x e y do primeiro ponto
printf("Coordenada x do primeiro ponto: ");
scanf("%f", &x1);
printf("Coordenada y do primeiro ponto: ");
scanf("%f", &y1);
// x e y do segundo ponto
printf("Coordenada x do segundo ponto: ");
scanf("%f", &x2);
printf("Coordenada y do segundo ponto: ");
scanf("%f", &y2);
// vamos calcular o coeficiente angular
m = (y2 - y1) / (x2 - x1);
// mostramos o resultado
printf("O coeficiente angular é: %f", m);
printf("\n\n");
system("PAUSE");
return 0;
}
Ao executar este código C nós teremos o seguinte resultado: Coordenada x do primeiro ponto: 3 Coordenada y do primeiro ponto: 6 Coordenada x do segundo ponto: 9 Coordenada y do segundo ponto: 10 O coeficiente angular é: 0.666667 Pressione qualquer tecla para continuar... Veja agora como podemos calcular o coeficiente angular da reta que passa pelos dois pontos usando o Teorema de Pitágoras. Note que agora nós estamos tirando proveito da tangente do ângulo Theta (__$\theta__$), também chamado de ângulo Alfa ou Alpha (__$\alpha__$):
#include <stdio.h>
#include <stdlib.h>
int main(int argc, char *argv[]){
// coordenadas dos dois pontos
float x1, y1, x2, y2;
// guarda os comprimentos dos catetos oposto e adjascente
float cateto_oposto, cateto_adjascente;
// guarda o ângulo tetha (em radianos) e a tangente
float tetha, tangente;
// x e y do primeiro ponto
printf("Coordenada x do primeiro ponto: ");
scanf("%f", &x1);
printf("Coordenada y do primeiro ponto: ");
scanf("%f", &y1);
// x e y do segundo ponto
printf("Coordenada x do segundo ponto: ");
scanf("%f", &x2);
printf("Coordenada y do segundo ponto: ");
scanf("%f", &y2);
// vamos obter o comprimento do cateto oposto
cateto_oposto = y2 - y1;
// e agora o cateto adjascente
cateto_adjascente = x2 - x1;
// vamos obter o ângulo tetha, ou seja, a inclinação da hipetunesa
// (em radianos, não se esqueça)
tetha = atan2(cateto_oposto, cateto_adjascente);
// e finalmente usamos a tangente desse ângulo para calcular
// o coeficiente angular
tangente = tan(tetha);
// mostramos o resultado
printf("O coeficiente angular é: %f", tangente);
printf("\n\n");
system("PAUSE");
return 0;
}
Ao executar este código você verá que o resultado é o mesmo. No entanto, fique atento às propriedades do coeficiente angular da reta: 1) O coeficiente angular é positivo quando a reta for crescente, ou seja, m > 0; 2) O coeficiente angular é negativo quando a reta for decrescente, ou seja, m < 0; 3) Se a reta estiver na horizontal, ou seja, paralela ao eixo x, seu coeficiente angular é zero (0). 4) Se a reta estiver na vertical, ou seja, paralela ao eixo y, o coeficiente angular não existe. |
Nossas 20 dicas & truques de programação mais populares |
Você também poderá gostar das dicas e truques de programação abaixo |
|
MySQL - Como retornar a hora atual no MySQL usando as funções CURTIME(), CURRENT_TIME e CURRENT_TIME() JavaScript - JavaScript para iniciantes - Como usar o método escape() para codificar uma frase em JavaScript |
Nossas 20 dicas & truques de programação mais recentes |
Últimos Projetos e Códigos Fonte Liberados Para Apoiadores do Site |
|
Python - Como criar o jogo Pedra, Papel, Tesoura em Python - Jogo completo em Python com código comentado |
Últimos Exercícios Resolvidos |
E-Books em PDF |
||||
|
||||
|
||||
Linguagens Mais Populares |
||||
|
1º lugar: Java |





