PHP ::: Dicas & Truques ::: Arquivos e Diretórios |
Como criar diretórios usando PHP - Como usar a função mkdir() da linguagem PHP para criar diretórios - RevisadaQuantidade de visualizações: 25201 vezes |
|
Diretórios podem ser criados com a função mkdir() do PHP. Esta função recebe o nome do diretório a ser criado, um modo que define as permissões de acesso ao diretório e um valor boolean que define se os diretórios fornecidos no primeiro parâmetro serão criados recursivamente. O valor padrão para o modo de acesso é 0777 (todos têm permissão de leitura, escrita e execução) e false para a criação de diretórios recursivamente. Veja um trecho de código no qual criamos um diretório no diretório public_html:
<?
// nome do diretório
$diretorio = "/site/public_html/minhas_imagens";
// cria o diretório com a permissão 0777
if(mkdir($diretorio))
echo "Diretório criado com sucesso.";
else
echo "Não foi possível criar o diretório.";
?>
Antes de criar um diretório, é preciso que você verifique se o diretório dentro do qual o novo diretório será criado apresenta as permissões adequadas, do contrário você terá a seguinte mensagem de erro: Warning: mkdir() [function.mkdir]: Permission denied in /site/public_html/testes.php on line 8 Não foi possível criar o diretório. Veja agora como criar um diretório contendo dois sub-diretórios recursivamente:
<?
// cria o diretório imagens contendo o subdiretório "fotos"
// e este conterá o sub-diretório
// "recentes"
$diretorio = "/site/public_html/imagens/fotos/recentes";
// cria o diretório com a permissão 0777
if(mkdir($diretorio, 0777, true))
echo "Diretório criado com sucesso.";
else
echo "Não foi possível criar o diretório.";
?>
Esta dica foi revisada, atualizada e testada com o PHP 8. |
Java ::: Dicas & Truques ::: Strings e Caracteres |
Como testar se duas strings são iguais em Java sem considerar letras maiúsculas e minúsculas usando o método equalsIgnoreCase()Quantidade de visualizações: 265 vezes |
|
Nesta dica mostrarei como podemos usar o método equalsIgnoreCase() da classe String da linguagem Java para verificar se duas palavras, frases ou textos são iguais desconsiderando letras maiúsculas e minúsculas. Veja o código completo para o exemplo:
package estudos;
public class Estudos{
public static void main(String[] args){
String s1 = "GOSTO de Java";
String s2 = "gosto de java";
System.out.println("A primeira string é: " + s1);
System.out.println("A segunda string é: " + s2);
if(s1.equalsIgnoreCase(s2)){
System.out.println("As duas strings sao iguais");
}
else{
System.out.println("As duas strings não sao iguais");
}
System.exit(0);
}
}
Ao executar este código Java nós teremos o seguinte resultado: A primeira string é: GOSTO de Java A segunda string é: gosto de java As duas strings são iguais |
Java ::: Fundamentos da Linguagem ::: Tipos de Dados |
Apostila de Java para iniciantes - Como usar o tipo de dados int da linguagem JavaQuantidade de visualizações: 12495 vezes |
O tipo de dados int pode ser usado quando queremos armazenar valores inteiros na faixa ?2.147.483.648 até 2.147.483.647 (acima de dois milhões). Veja um exemplo:
public class Estudos{
static int valor = 1500;
public static void main(String args[]){
System.out.println("O valor da variável é: "
+ valor);
System.exit(0);
}
}
O tipo de dados int pode ser convertido (sem a necessidade de cast) para os seguintes tipos: int -> long -> float -> double Se precisarmos converter o tipo int para os tipos char, byte ou short, teremos que lançar mão de uma coerção (cast). Veja: short valor2 = (short)(valor); |
Delphi ::: Dicas & Truques ::: Strings e Caracteres |
Como substituir todas as ocorrências de uma substring em uma string em Delphi sem considerar maiúsculas e minúsculas usando a função ReplaceText()Quantidade de visualizações: 11993 vezes |
Algumas vezes precisamos substituir todas as ocorrências de uma substring em uma string mas não queremos diferenciar letras maiúsculas de letras minúsculas. Em Delphi isso pode ser feito com o auxílio da função ReplaceText(). Esta função requer a string na qual a substituição ocorrerá, a substring a ser substituída e a nova substring. O resultado será uma nova string resultante da substituição. Veja o exemplo:procedure TForm1.Button1Click(Sender: TObject); var frase: string; begin frase := 'PHP? Sim, eu gosto muito de PHP'; // vamos substituir todas as ocorrências de "PHP" por "Delphi' // sem considerar maiúsculas e minúsculas frase := ReplaceText(frase, 'Php', 'Delphi'); // vamos exibir o resultado ShowMessage(frase); end; Lembre-se de que esta função não diferencia maiúsculas e minúsculas. Não se esqueça de adicionar a unit StrUtils no uses do seu formulário. Para questões de compatibilidade, esta dica foi escrita usando Delphi 2009. |
C# ::: Dicas & Truques ::: Trigonometria - Funções Trigonométricas |
Como calcular o cosseno de um ângulo em C# usando a função Cos() da classe Math - Calculadora de cosseno em C#Quantidade de visualizações: 2099 vezes |
|
Em geral, quando falamos de cosseno, estamos falando do triângulo retângulo de Pitágoras (Teorema de Pitágoras). A verdade é que podemos usar a função cosseno disponível nas linguagens de programação para calcular o cosseno de qualquer número, mesmo nossas aplicações não tendo nenhuma relação com trigonometria. No entanto, é sempre importante entender o que é a função cosseno. Veja a seguinte imagem:  Veja que temos um triângulo retângulo com as medidas já calculadas para a hipotenusa e os dois catetos, assim como os ângulos entre eles. Assim, o cosseno é a razão entre o cateto adjascente e a hipotenusa, ou seja, o cateto adjascente dividido pela hipotenusa. Veja a fórmula: \[\text{Cosseno} = \frac{\text{Cateto adjascente}}{\text{Hipotenusa}} \] Então, se dividirmos 30 por 36.056 (na figura eu arredondei) nós teremos 0.8320, que é a razão entre o cateto adjascente e a hipotenusa (em radianos). Agora, experimente calcular o arco-cosseno de 0.8320. O resultado será 0.5881 (em radianos). Convertendo 0.5881 radianos para graus, nós obtemos 33.69º, que é exatamente o ângulo em graus entre o cateto adjascente e a hipotenusa na figura acima. Pronto! Agora que já sabemos o que é cosseno na trigonometria, vamos entender mais sobre a função Cos() da linguagem C#. Esta função, que é um método da classe Math, recebe um valor numérico Double e retorna um valor Double, ou seja, também numérico) entre -1 até 1 (ambos inclusos). Veja:
using System;
using System.Collections;
namespace Estudos {
class Program {
static void Main(string[] args) {
// vamos calcular o cosseno de três números
Console.WriteLine("Cosseno de 0 = " + Math.Cos(0));
Console.WriteLine("Cosseno de 1 = " + Math.Cos(1));
Console.WriteLine("Cosseno de 2 = " + Math.Cos(2));
Console.WriteLine("\nPressione qualquer tecla para sair...");
// pausa o programa
Console.ReadKey();
}
}
}
Ao executar este código C# nós teremos o seguinte resultado: Cosseno de 0 = 1 Cosseno de 1 = 0,5403023058681397 Cosseno de 2 = -0,4161468365471424 Note que calculamos os cossenos dos valores 0, 1 e 2. Observe como os resultados conferem com a curva da função cosseno mostrada abaixo: 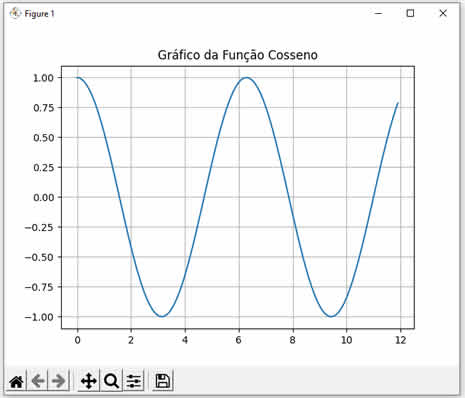 |
Dart ::: Dicas & Truques ::: Trigonometria - Funções Trigonométricas |
Como calcular o cosseno de um ângulo em Dart usando o método cos() da biblioteca Math - Calculadora de cosseno em DartQuantidade de visualizações: 877 vezes |
|
Em geral, quando falamos de cosseno, estamos falando do triângulo retângulo de Pitágoras (Teorema de Pitágoras). A verdade é que podemos usar a função cosseno disponível nas linguagens de programação para calcular o cosseno de qualquer número, mesmo nossas aplicações não tendo nenhuma relação com trigonometria. No entanto, é sempre importante entender o que é a função cosseno. Veja a seguinte imagem:  Veja que temos um triângulo retângulo com as medidas já calculadas para a hipotenusa e os dois catetos, assim como os ângulos entre eles. Assim, o cosseno é a razão entre o cateto adjascente e a hipotenusa, ou seja, o cateto adjascente dividido pela hipotenusa. Veja a fórmula: \[\text{Cosseno} = \frac{\text{Cateto adjascente}}{\text{Hipotenusa}} \] Então, se dividirmos 30 por 36.056 (na figura eu arredondei) nós teremos 0.8320, que é a razão entre o cateto adjascente e a hipotenusa (em radianos). Agora, experimente calcular o arco-cosseno de 0.8320. O resultado será 0.5881 (em radianos). Convertendo 0.5881 radianos para graus, nós obtemos 33.69º, que é exatamente o ângulo em graus entre o cateto adjascente e a hipotenusa na figura acima. Pronto! Agora que já sabemos o que é cosseno na trigonometria, vamos entender mais sobre a função cos() da linguagem Dart. Esta método, que faz parte da biblioteca Math, recebe um valor numérico e retorna um valor, também numérico) entre -1 até 1 (ambos inclusos). Veja:
// vamos importar a biblioteca dart:math
import "dart:math";
void main(){
print("Cosseno de 0 = " + cos(0).toString());
print("Cosseno de 1 = " + cos(1).toString());
print("Cosseno de 2 = " + cos(2).toString());
}
Ao executar este código Dart nós teremos o seguinte resultado: Cosseno de 0 = 1.0 Cosseno de 1 = 0.5403023058681398 Cosseno de 2 = -0.4161468365471424 Note que calculamos os cossenos dos valores 0, 1 e 2. Observe como os resultados conferem com a curva da função cosseno mostrada abaixo:  |
Java ::: Estruturas de Dados ::: Árvore Binária e Árvore Binária de Busca |
Estruturas de Dados em Java - Como obter o nó com menor valor em uma árvore binária de busca em JavaQuantidade de visualizações: 3446 vezes |
Em exemplos dessa seção nós vimos como criar árvores binárias e árvores binárias de busca em Java e como pesquisar ou fazer a sua travessia, visitando cada um dos nós. Nesta dica mostrarei como obter o nó com o menor valor em uma árvore binária. O truque aqui é descer o lado esquerdo da árvore até o último nó. Veja:
// método que permite retornar o menor nó de uma árvore
// binária de busca
public No retornarMenorElemento(){
// chama a versão recursiva do método
return retornarMenorElemento(raiz);
}
public No retornarMenorElemento(No no){
if((no == null) || (no.getEsquerdo() == null)){
return no; // ponto de parada
}
else{ // vamos continuar descendo do lado esquerdo
return retornarMenorElemento(no.getEsquerdo());
}
}
Este método faz parte da classe ArvoreBinariaBusca.java. Veja agora como chamá-lo a partir da classe principal, ou seja, a classe de teste:
package arvore_binaria;
import java.util.Scanner;
public class ArvoreBinariaTeste {
public static void main(String[] args) {
Scanner entrada = new Scanner(System.in);
// vamos criar um novo objeto da classe ArvoreBinariaBusca
ArvoreBinariaBusca arvore = new ArvoreBinariaBusca();
// vamos inserir 5 valores na árvore
for(int i = 0; i < 5; i++){
System.out.print("Informe um valor inteiro: ");
int valor = Integer.parseInt(entrada.nextLine());
// vamos inserir o nó e verificar o sucesso da operação
if(!arvore.inserir(valor)){
System.out.println("Não foi possível inserir." +
" Um elemento já contém este valor.");
}
}
// vamos o menor elemento na árvore binária de busca
System.out.println("\nO menor nó é: " +
arvore.retornarMenorElemento().getValor());
System.out.println("\n");
}
}
Ao executar este código teremos o seguinte resultado: Informe um valor inteiro: 5 Informe um valor inteiro: 12 Informe um valor inteiro: 87 Informe um valor inteiro: 1 Informe um valor inteiro: 3 O menor nó é: 1 |
PHP ::: Dicas & Truques ::: Matemática e Estatística |
Como resolver uma equação do segundo grau em PHP - Como calcular Bhaskara em PHPQuantidade de visualizações: 1235 vezes |
|
Como resolver uma equação do 2º grau usando PHP Nesta dica mostrarei como encontrar as raízes de uma equação quadrática, ou seja, uma equação do 2º usando a linguagem PHP. Definimos como equação do 2º grau ou equações quadráticas qualquer equação do tipo ax² + bx + c = 0 em que a, b e c são números reais e a ≠ 0. Ela recebe esse nome porque, no primeiro membro da igualdade, há um polinômio de grau dois com uma única incógnita. Note que, dos coeficientes a, b e c, somente o a é diferente de zero, pois, caso ele fosse igual a zero, o termo ax² seria igual a zero, logo a equação se tornaria uma equação do primeiro grau: bx + c = 0. Independentemente da ordem da equação, o coeficiente a sempre acompanha o termo x², o coeficiente b sempre acompanha o termo x, e o coeficiente c é sempre o termo independente. Como resolver uma equação do 2º grau Conhecemos como soluções ou raízes da equação ax² + bx + c = 0 os valores de x que fazem com que essa equação seja verdadeira. Uma equação do 2º grau pode ter no máximo dois números reais que sejam raízes dela. Para resolver equações do 2º grau completas, existem dois métodos mais comuns: a) Fórmula de Bhaskara; b) Soma e produto. O primeiro método é bastante mecânico, o que faz com que muitos o prefiram. Já para utilizar o segundo, é necessário o conhecimento de múltiplos e divisores. Além disso, quando as soluções da equação são números quebrados, soma e produto não é uma alternativa boa. Como resolver uma equação do 2º grau usando Bhaskara Como nosso código PHP vai resolver a equação quadrática usando a Fórmula de Bhaskara, o primeiro passo é encontrar o determinante. Veja: \[\Delta =b^2-4ac\] Nem sempre a equação possui solução real. O valor do determinante é que nos indica isso, existindo três possibilidades: a) Se determinante > 0, então a equação possui duas soluções reais. b) Se determinante = 0, então a equação possui uma única solução real. c) Se determinante < 0, então a equação não possui solução real. Encontrado o determinante, só precisamos substituir os valores, incluindo o determinante, na Fórmula de Bhaskara: \[x = \dfrac{- b\pm\sqrt{b^2- 4ac}}{2a}\] Vamos agora ao código PHP. Nossa aplicação vai pedir para o usuário informar os valores dos três coeficientes a, b e c e, em seguida, vai apresentar as raizes da equação:
<?php
// para executar abra uma janela de comando
// cmd e dispare o comando abaixo:
// C:\xampp\php>php c:\estudos_php\estudos.php
// para ler a entrada do usuário
$entrada = fopen("php://stdin","r");
// vamos pedir para o usuário informar os valores dos coeficientes
echo "Valor do coeficiente a: ";
$a = trim(fgets($entrada));
echo "Valor do coeficiente b: ";
$b = trim(fgets($entrada));
echo "Valor do coeficiente c: ";
$c = trim(fgets($entrada));
// vamos calcular o discriminante
$discriminante = ($b * $b) - (4 * $a * $c);
// a equação possui duas soluções reais?
if($discriminante > 0){
$raiz1 = (-$b + sqrt($discriminante)) / (2 * $a);
$raiz2 = (-$b - sqrt($discriminante)) / (2 * $a);
echo "Existem duas raizes: x1 = " . $raiz1 .
" e x2 = " . $raiz2;
}
// a equação possui uma única solução real?
else if($discriminante == 0){
$raiz1 = $raiz2 = -$b / (2 * $a);
echo "Existem duas raizes iguais: x1 = " . $raiz1 .
" e x2 = " . $raiz2;
}
// a equação não possui solução real?
else if($discriminante < 0){
$raiz1 = $raiz2 = -$b / (2 * $a);
$imaginaria = sqrt(-$discriminante) / (2 * $a);
echo "Existem duas raízes complexas: x1 = " . $raiz1 .
" + " . $imaginaria . " e x2 = " . $raiz2 . " - " . $imaginaria;
}
?>
Ao executar este código PHP nós teremos o seguinte resultado: Valor do coeficiente a: 1 Valor do coeficiente b: 2 Valor do coeficiente c: -3 Existem duas raizes: x1 = 1 e x2 = -3 |
Python ::: Python para Engenharia ::: Geometria Analítica e Álgebra Linear |
Python para Engenharia - Como multiplicar um vetor por um escalar usando Python e NumPyQuantidade de visualizações: 3461 vezes |
|
Esta dica de Python e NumPy é direcionada, principalmente, aos estudantes de Engenharia, que se deparam, logo no início do curso, com o estudo da Geometria Analítica e gostariam de entender melhor a multiplicação de vetores por um escalar. Lembre-se de que um escalar é um valor único, enquanto vetores e matrizes são estruturas que guardam vários valores ao mesmo tempo. Nosso primeiro exemplo será feito em cima de um vetor no R3, ou seja, no espaço, com os seguintes valores: [3, -5, 4]. O escalar usado será o valor 2, ou seja, temos que multiplicar cada valor no vetor pelo valor 2 e, dessa forma, obtermos um novo vetor, também no R3. Vetores no R3 possuem valores para x, y e z (três dimensões), enquanto vetores no R2 possuem apenas o x e y. Veja como a linguagem Python facilita a operação da multiplicação de um vetor R3 por um escalar:
# importamos a bibliteca NumPy
import numpy as np
def main():
# declara e cria o vetor
vetor = np.array([3, -5, 4])
# agora vamos multiplicar este vetor pelo escalar 2
escalar = 2
novoVetor = vetor * escalar
# vamos exibir o resultado
print("Vetor inicial: ", vetor)
print("Valor do escalar: ", escalar)
print("Novo vetor: ", novoVetor)
if __name__== "__main__":
main()
Este código Python vai gerar o seguinte resultado: Vetor inicial: [3 -5 4] Valor do escalar: 2 Novo vetor: [6 -10 8] Agora, saindo da Geometria Analítica e indo para a Álgebra Linear, veja como podemos efetuar a mesma operação em uma matriz de 2 linhas e 3 colunas (recorde que, em Python, uma matriz nada mais é do que um vetor de vetores, ou seja, cada elemento do vetor contém outro vetor):
# importamos a bibliteca NumPy
import numpy as np
def main():
# declara e cria a matriz
matriz = np.array([(4, 12, 50), (5, 3, 1), (11, 9, 7)])
# agora vamos multiplicar esta matriz pelo escalar 2
escalar = 2
novaMatriz = matriz * escalar
# vamos exibir o resultado
print("Matriz inicial: ", matriz)
print("Valor do escalar: ", escalar)
print("Nova matriz: ", novaMatriz)
if __name__== "__main__":
main()
Ao executarmos este código Python nós teremos o seguinte resultado: Matriz inicial: [[4 12 50] [5 3 1] [11 9 7]] Valor do escalar: 2 Nova matriz: [[8 24 100] [10 6 2] [22 18 14]] |
Java ::: Pacote java.util ::: Iterator |
Como usar o método next() da interface Iterator do Java para obter o próximo elemento da iteraçãoQuantidade de visualizações: 4219 vezes |
O método next() da interface Iterator é usado quando queremos acessar o próximo elemento de uma iteração. Veja sua assinatura:E next() Veja que o tipo retornado equivale ao tipo do elemento usado na declaração do iterador. Veja um exemplo:
package estudos;
import java.util.ArrayList;
import java.util.Iterator;
public class Estudos{
public static void main(String[] args) {
// vamos criar uma ArrayList
ArrayList<String> pessoas = new ArrayList();
pessoas.add("Osmar");
pessoas.add("Carlos");
pessoas.add("Fernanda");
// vamos obter um iterador para a lista
Iterator<String> pessoa = pessoas.iterator();
// vamos obter o próximo elemento (neste caso, o primeiro)
String s1 = pessoa.next();
System.out.println(s1);
// vamos obter o próximo elemento (o segundo)
String s2 = pessoa.next();
System.out.println(s2);
// vamos obter o próximo elemento (o terceiro)
String s3 = pessoa.next();
System.out.println(s3);
// vamos obter o próximo elemento (vai dar erro. não há um quarto elemento)
String s4 = pessoa.next();
System.out.println(s4);
}
}
Ao executarmos este código nós teremos o seguinte resultado: Osmar Carlos Fernanda Exception in thread "main" java.util.NoSuchElementException at java.util.ArrayList$Itr.next(ArrayList.java:834) at estudos.Estudos.main(Estudos.java:30) Java Result: 1 Veja que o método next() atira uma exceção do tipo NoSuchElementException se o iterador não possuir mais elementos. |
Nossas 20 dicas & truques de programação mais populares |
Você também poderá gostar das dicas e truques de programação abaixo |
Nossas 20 dicas & truques de programação mais recentes |
Últimos Projetos e Códigos Fonte Liberados Para Apoiadores do Site |
|
Python - Como criar o jogo Pedra, Papel, Tesoura em Python - Jogo completo em Python com código comentado |
Últimos Exercícios Resolvidos |
E-Books em PDF |
||||
|
||||
|
||||
Linguagens Mais Populares |
||||
|
1º lugar: Java |






